Ο "ανατοκισμός" είναι μια λέξη που χρησιμοποιείται συχνά στον κόσμο των αποταμιεύσεων και των επενδύσεων. Παρόλο που το νόημά της μπορεί να μην είναι άμεσα προφανές, είναι στην πραγματικότητα αρκετά εύκολο να την κατανοήσεις και μπορεί να έχει σημαντική επίδραση στα οικονομικά σου. Αυτή η σχετικά απλή έννοια σχετίζεται τόσο με τις αποταμιεύσεις όσο και με τα χρέη σας και ως εκ τούτου είναι κάτι που πρέπει να εξετάζει όποιος σχεδιάζει το οικονομικό του μέλλον.
Πάμε να δούμε το φαινόμενο του ανατοκισμού πιο προσεκτικά.
Πώς Δουλεύει ο Ανατοκισμός
Ο ανατοκισμός αναφέρεται στην αρχή ότι όταν αποταμιεύεις χρήματα, εκτός από τους τόκους των αποταμιεύσεών σου, κερδίζεις τόκους και από τους ίδιους τους τόκους. Αυτό σημαίνει ότι κάθε χρόνο που τα χρήματά σου βρίσκονται στον λογαριασμό, κερδίζεις τόκους επί των τόκων κάθε προηγούμενου έτους. Έτσι, όχι μόνο οι αποταμιεύσεις σου αυξάνονται με την πάροδο του χρόνου, αλλά και ο ρυθμός με τον οποίο αυξάνονται γίνεται ταχύτερος.
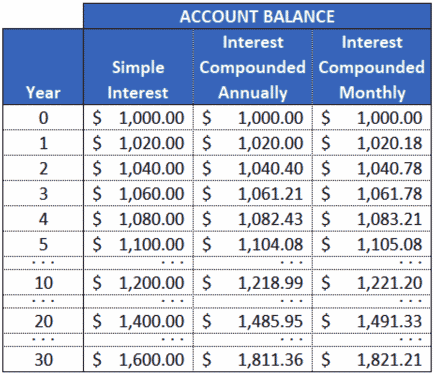
Ο ρυθμός με τον οποίο συσσωρεύεται ο σύνθετος τόκος (ή "ανατοκισμός", όπως λέγεται μερικές φορές) εξαρτάται επίσης από τη συχνότητα των πληρωμών των τόκων. Αν η περίοδος επιτοκίου δεν είναι ετήσια, αλλά εξαμηνιαία, τριμηνιαία ή μηνιαία, τότε το συνολικό ποσό των τόκων που θα λάβεις κατά τη διάρκεια του έτους θα είναι υψηλότερο. Αυτό συμβαίνει επειδή οι τόκοι υπολογίζονται πάνω στους τόκους που συσσωρεύονται σε αυτές τις μικρότερες περιόδους.
Πρακτικό Παράδειγμα
Ας υποθέσουμε ότι μια πολύ γενναιόδωρη τράπεζα (τη δεκαετία του 90 ίσως και να ίσχυε) προσφέρει στον Νίκο και τη Μαρία απόδοση 10% ετησίως, και ο καθένας από αυτούς επενδύει 1.000 ευρώ, το οποίο ονομάζεται αρχικό κεφάλαιο. Ο Νίκος θέλει να ξοδεύει τους τόκους κάθε χρόνο και να κρατά μόνο το αρχικό κεφάλαιο στην τράπεζα, ενώ η Μαρία θέλει να αποταμιεύσει για 30 χρόνια, χωρίς να βγάζει τους τόκους κάθε χρόνο.
Στην περίπτωση του Νίκου, το 10% ανέρχεται σε 100 ευρώ κάθε χρόνο, οπότε μετά από έναν χρόνο θα έχει 1.100 ευρώ στον λογαριασμό του, από τα οποία θα πάρει 100 ευρώ. Μετά τον δεύτερο χρόνο, θα έχει ξανά 1.100 ευρώ στον λογαριασμό του, από τα οποία θα πάρει πάλι 100 ευρώ. Μετά από τον τριακοστό χρόνο, θα έχει 1.100 ευρώ όπως πάντα και θα πάρει τα 100 ευρώ, αφήνοντάς τον με 1.000 ευρώ στον λογαριασμό του. Έτσι, το αρχικό του κεφάλαιο και οι τόκοι που έβγαλε ανέρχονται σε 100 ευρώ επί 30 χρόνια, δηλαδή συνολικά 3.000 ευρώ. Με άλλα λόγια, το συνολικό ποσό που έβγαλε σε 30 χρόνια είναι 4.000 ευρώ.
Η Μαρία, από την άλλη, θα κερδίσει περισσότερα. Μετά από έναν χρόνο, θα έχει 1.100 ευρώ στον λογαριασμό της, αλλά τα κρατάει όλα εκεί. Μετά τον δεύτερο χρόνο, θα κερδίσει 10% επί των 1.100 ευρώ, και όχι μόνο επί των αρχικών 1.000 ευρώ. Επομένως, θα έχει 1.100 ευρώ συν 110 ευρώ, δηλαδή 1.210 ευρώ. Μετά τον τρίτο χρόνο, θα κερδίσει 10% επί των 1.210 ευρώ και θα έχει 1.331 ευρώ.
Μετά από 30 χρόνια, η Μαρία θα έχει 17.449,40 ευρώ, πάνω από τέσσερις φορές περισσότερα από τον Νίκο. Αυτό είναι με απλά λόγια το φαινόμενο του ανατοκισμού, χωρίς φυσικά να υπολογίζουμε φόρους και πληθωρισμό.
Η Δύναμη του Ανατοκισμού: Γιατί Ο Χρόνος Είναι Χρήμα
Η έννοια του ανατοκισμού είναι ισχυρή, γιατί ακόμη και αν δεν προσθέτεις στις αποταμιεύσεις σου, αυτές μπορούν να συνεχίσουν να αυξάνονται. Σε μια μακροχρόνια περίοδο, αυτό μπορεί να δημιουργήσει μια τεράστια διαφορά και εξηγεί γιατί τόσοι πολλοί ειδικοί συμβουλεύουν να ξεκινήσεις να αποταμιεύεις νωρίς.
Αν, για παράδειγμα, άρχιζες να αποταμιεύεις 100 ευρώ τον μήνα στην ηλικία των 30 και συνέχιζες μέχρι τα 60, με ετήσιο επιτόκιο 10%*, θα είχες μαζέψει περίπου 217.132,11 ευρώ. Ωστόσο, αν ξεκινούσες να αποταμιεύεις 100 ευρώ τον μήνα από τα 20 σου και σταματούσες στα 30, αλλά άφηνες τα χρήματα στο λογαριασμό μέχρι τα 60, θα είχες συγκεντρώσει 367.090,06 ευρώ.
Η "μαγεία" του ανατοκισμού σε αυτό το παράδειγμα δείχνει ότι η αποταμίευση για 10 χρόνια μπορεί να είναι πιο αποδοτική από την αποταμίευση για 30 χρόνια, αν ξεκινήσεις νωρίτερα. Αν και το παραπάνω είναι ένα απλό υποθετικό παράδειγμα που μπορείς εύκολα να υπολογίσεις με έναν υπολογιστή ανατοκισμού ή ένα υπολογιστικό φύλλο, σε πραγματικές περιπτώσεις μπορεί να δεις παρόμοια αποτελέσματα.
Βέβαια, υπάρχουν και άλλοι παράγοντες, όπως ο πληθωρισμός, οι διακυμάνσεις των επιτοκίων, καθώς και αναλήψεις ή καταθέσεις που θα επηρεάσουν το πώς θα αυξάνονται οι αποταμιεύσεις σου.
*Το επιτόκιο 10% χρησιμοποιείται για την ευκολία της κουβέντας – οι πραγματικές αποδόσεις του χρηματιστηρίου ενδέχεται να είναι αρκετά χαμηλότερες. Επίσης στον πραγματικό κόσμο υπάρχει πληθωρισμός και φόροι που μειώνουν ακόμα περισσότερο τις αποδόσεις. Ωστόσο οι αρχές παραμένουν οι ίδιες.
Ανατοκισμός Χρέους: Η Άλλη Όψη του Ίδιου Νομίσματος
Παρόλο που ο σύνθετος τόκος μπορεί να προσφέρει σημαντικά οφέλη στους επενδυτές, η ίδια αρχή εφαρμόζεται και στους τόκους που πληρώνεις για τα χρέη σου. Όταν κάνεις αποπληρωμές σε μια πιστωτική κάρτα, πληρώνεις τόκους όχι μόνο για το αρχικό χρέος, αλλά και για τους τόκους που έχουν ήδη συσσωρευτεί. Με τον ίδιο τρόπο που ένα μικρό ποσό αποταμίευσης μπορεί να αυξηθεί με τον χρόνο χωρίς επιπλέον καταθέσεις, ένα μικρό χρέος μπορεί επίσης να αυξηθεί χωρίς περαιτέρω δαπάνες.
Η έννοια του ανατοκισμού δεν είναι ιδιαίτερα περίπλοκη, αλλά μπορεί εύκολα να υποτιμήσεις την επίδρασή του. Ναι μεν αυτό μπορεί να είναι μια ευχάριστη έκπληξη όταν οι αποταμιεύσεις/επενδύσεις σου αυξάνονται πιο γρήγορα από το αναμενόμενο, αλλά μπορεί να έχει αρνητικές συνέπειες αν δεν συνειδητοποιήσεις το συνολικό ποσό που θα χρειαστεί να αποπληρώσεις, αν κάνεις μικρές πληρωμές για πολλά χρόνια. Για αυτό και πάντα πληρώνουμε ολόκληρο το οφειλόμενο ποσό σε πιστωτικές κάρτες και όχι την ελάχιστη δυνατή καταβολή.
Αρνητικά και Θετικά
Η δύναμή του έγκειται στο λεγόμενο "φαινόμενο της χιονoστιβάδας". Ακόμη και μικρές επενδύσεις μπορούν, με τον καιρό, να αποφέρουν μεγάλες αποδόσεις μέσω του ανατοκισμού. Το φαινόμενο της χιονοστιβάδας είναι ιδιαίτερα ευεργετικό για σένα, αν αρχίσεις αρκετά νωρίς. Παρόλο που αρχικά θα έχεις συγκεντρώσει λιγότερα χρήματα από τις τακτικές επενδύσεις, θα έχεις ένα σημαντικό ποσό μέχρι τη στιγμή που θα συνταξιοδοτηθείς.
Ένα από τα μειονεκτήματα του ανατοκισμού είναι ότι τα πλεονεκτήματά του ισχύουν και για τα χρηματοπιστωτικά ιδρύματα. Οι δανειστές και οι εκδότες πιστωτικών καρτών μπορούν να χρησιμοποιούν τον σύνθετο τόκο για την αποπληρωμή των φοιτητικών δανείων και των χρεών πιστωτικών καρτών σου. Αυτός ο τόκος μπορεί να αυξάνεται ανεξέλεγκτα με τον χρόνο, ειδικά αν πληρώνεις μόνο το ελάχιστο μηνιαίο ποσό. Ο σύνθετος τόκος υπολογίζεται πάντα πριν κάνεις την πληρωμή, όχι μετά. Αν καθυστερήσεις ή χάσεις μια πληρωμή, μπορεί να σου κοστίσει περισσότερα χρήματα.
Ποιός Είναι ο Ρόλος του Ανατοκισμού στις Επενδύσεις
Ο ανατοκισμός εφαρμόζεται επίσης στις επενδύσεις. Για παράδειγμα, ένας επενδυτής που συμμετέχει σε ένα πρόγραμμα επανεπένδυσης μερισμάτων (DRIP) χρησιμοποιεί τον ανατοκισμό για να αυξήσει την αξία της επένδυσής του. Τα μερίσματα που λαμβάνει ο επενδυτής επανεπενδύονται για την αγορά περισσότερων μετοχών, με αποτέλεσμα να κερδίζει τόκους πάνω σε μεγαλύτερη επένδυση.
Παρόμοια, τα ομόλογα μηδενικού κουπονιού εκμεταλλεύονται τον ανατοκισμό. Αυτά τα ομόλογα δεν πληρώνουν περιοδικούς τόκους όπως τα παραδοσιακά, αλλά αγοράζονται σε χαμηλότερη τιμή και η αξία τους αυξάνεται με την πάροδο του χρόνου. Στη λήξη τους, φτάνουν την πλήρη τιμή, κάτι που είναι αποτέλεσμα της συσσώρευσης των τόκων μέσω του σύνθετου τόκου.
Υπολογίζοντας τον Ανατοκισμό
Μπορείς να χρησιμοποιήσεις διάφορα εργαλεία για να υπολογίσεις τον σύνθετο τόκο, συμπεριλαμβανομένου του Microsoft Excel ή του Google Sheets, το οποίο μπορείς να χρησιμοποιήσεις με τρεις διαφορετικούς τρόπους:
Προσέγγιση 1: Πολλαπλασιασμός
Ο πρώτος τρόπος για να υπολογίσεις τον σύνθετο τόκο είναι να πολλαπλασιάζεις το νέο υπόλοιπο κάθε χρονιάς με το επιτόκιο.
Ας υποθέσουμε ότι καταθέτεις 1.000 δολάρια σε έναν λογαριασμό ταμιευτηρίου με ετήσιο επιτόκιο 5% που ανατοκίζεται κάθε χρόνο, και θέλεις να υπολογίσεις το υπόλοιπο σε πέντε χρόνια.
Στο Microsoft Excel, πληκτρολόγησε «Έτος» στο κελί Α1 και «Υπόλοιπο» στο κελί Β1.
Εισήγαγε τα έτη από 0 έως 5 στα κελιά Α2 έως Α7.
Το υπόλοιπο για το έτος 0 είναι 1.000 δολάρια, οπότε εισήγαγε «1000» στο κελί Β2.
Στη συνέχεια, εισήγαγε «=B2*1.05» στο κελί Β3.
Στη συνέχεια, εισήγαγε «=B3*1.05» στο κελί Β4 και συνέχισε με τον ίδιο τρόπο μέχρι το κελί Β7.
Στο κελί Β7, ο υπολογισμός είναι «=B6*1.05».
Τελικά, η τιμή που υπολογίζεται στο κελί Β7—$1.276,28—είναι το υπόλοιπο στον λογαριασμό σου μετά από πέντε χρόνια.
Για να βρεις την αξία του σύνθετου τόκου, αφαίρεσε τα 1.000 δολάρια από τα 1.276,28 δολάρια. Το αποτέλεσμα είναι 276,28 δολάρια.
Προσέγγιση 2: Σταθερός τύπος
Ο δεύτερος τρόπος για να υπολογίσεις τον σύνθετο τόκο είναι με έναν σταθερό τύπο.
Ο τύπος του σύνθετου τόκου είναι ((P*(1+i)^n) - P), όπου P είναι το αρχικό κεφάλαιο, i είναι το ετήσιο επιτόκιο και n είναι ο αριθμός των περιόδων.
Χρησιμοποιώντας τις ίδιες οικονομικές πληροφορίες όπως στην Προσέγγιση 1, πληκτρολόγησε «Κεφάλαιο» στο κελί Α1 και «1000» στο κελί Β1.
Στη συνέχεια, πληκτρολόγησε «Επιτόκιο» στο κελί Α2 και «.05» στο κελί Β2.
Εισήγαγε «Περίοδοι ανατοκισμού» στο κελί Α3 και «5» στο κελί Β3.
Τώρα μπορείς να υπολογίσεις τον σύνθετο τόκο στο κελί Β4 εισάγοντας «=(B1*(1+B2)^B3)-B1», το οποίο σου δίνει 276,28 δολάρια.
Online Υπολογιστές Ανατοκισμού
Μπορείς επίσης να χρησιμοποιήσεις αρκετούς δωρεάν online υπολογιστές ανατοκισμού.
Investor.gov Compound Interest Calculator: Αυτός ο δωρεάν υπολογιστής από την Επιτροπή Κεφαλαιαγοράς των ΗΠΑ (SEC) είναι απλός στη χρήση και επιτρέπει εισαγωγή μηνιαίων πρόσθετων καταθέσεων, για να υπολογίσεις τα κέρδη όταν κάνεις μηνιαίες αποταμιεύσεις.
TheCalculatorSite.com Compound Interest Calculator: Αυτός ο υπολογιστής υποστηρίζει πέντε διαφορετικά νομίσματα, υπολογίζει μηνιαίες καταθέσεις ή αναλήψεις, και προσφέρει αυτόματο υπολογισμό προσαρμοσμένο στον πληθωρισμό για μηνιαίες καταθέσεις ή αναλήψεις.
Council for Economic Education Compound Interest Calculator: Αυτός ο υπολογιστής είναι προσανατολισμένος σε μαθητές και δείχνει τη μακροπρόθεσμη δύναμη του ανατοκισμού. Εισάγεις την ηλικία σου, το ετήσιο επιτόκιο, την αρχική επένδυση και τις μηνιαίες αποταμιεύσεις. Το διάγραμμα που προκύπτει δείχνει πώς τα χρήματά σου αυξάνονται με τον χρόνο και τη διαφορά μεταξύ συνολικών αποδόσεων και αρχικού κεφαλαίου.
Συμπέρασμα
Η μακροπρόθεσμη επίδραση του ανατοκισμού στις αποταμιεύσεις και τις επενδύσεις είναι πράγματι σημαντική. Καθώς αυξάνει τα χρήματά σου πολύ πιο γρήγορα από τον απλό τόκο, ο ανατοκισμός παίζει κεντρικό ρόλο στην αύξηση του πλούτου. Επιπλέον, μπορεί να σε βοηθήσει να αντιμετωπίσεις την αύξηση του κόστους ζωής που προκαλεί ο πληθωρισμός.
Για τους νέους, ο σύνθετος τόκος προσφέρει μια σπουδαία ευκαιρία να επωφεληθούν από τη δύναμη της χρονικής αξίας του χρήματος. Να θυμάσαι, όταν επιλέγεις επενδύσεις, ότι ο αριθμός των περιόδων ανατοκισμού είναι εξίσου σημαντικός με το επιτόκιο.
